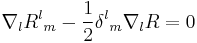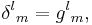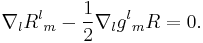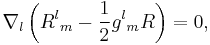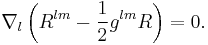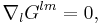Proofs involving covariant derivatives

Proof 1

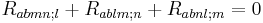$R_{abmn;l} %2B R_{ablm;n} %2B R_{abnl;m} = 0\,\!$ .

Contract both sides of the above equation with a pair of metric tensors:

$g^{bn} g^{am} (R_{abmn;l} %2B R_{ablm;n} %2B R_{abnl;m}) = 0,\,\!$

$g^{bn} (R^m {}_{bmn;l} - R^m {}_{bml;n} %2B R^m {}_{bnl;m}) = 0,\,\!$

$g^{bn} (R_{bn;l} - R_{bl;n} - R_b {}^m {}_{nl;m}) = 0,\,\!$

$R^n {}_{n;l} - R^n {}_{l;n} - R^{nm} {}_{nl;m} = 0.\,\!$

The first term on the left contracts to yield a Ricci scalar, while the third term contracts to yield a mixed Ricci tensor,

$R_{;l} - R^n {}_{l;n} - R^m {}_{l;m} = 0.\,\!$

The last two terms are the same (changing dummy index n to m) and can be combined into a single term which shall be moved to the right,

$R_{;l} = 2 R^m {}_{l;m},\,\!$

which is the same as

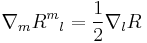$\nabla_m R^m {}_l = {1 \over 2} \nabla_l R\,\!$ .

Swapping the index labels l and m yields

$\nabla_l R^l {}_m = {1 \over 2} \nabla_m R\,\!$ , Q.E.D. (return to article)

The last equation in Proof 1 above can be expressed as

$\nabla_l R^l {}_m - {1 \over 2} \delta^l {}_m \nabla_l R = 0\,\!$

where δ is the Kronecker delta. Since the mixed Kronecker delta is equivalent to the mixed metric tensor,

$\delta^l {}_m = g^l {}_m,\,\!$

and since the covariant derivative of the metric tensor is zero (so it can be moved in or out of the scope of any such derivative), then

$\nabla_l R^l {}_m - {1 \over 2} \nabla_l g^l {}_m R = 0.\,\!$

Factor out the covariant derivative

$\nabla_l \left(R^l {}_m - {1 \over 2} g^l {}_m R\right) = 0,\,\!$

then raise the index m throughout

$\nabla_l \left(R^{lm} - {1 \over 2} g^{lm} R\right) = 0.\,\!$

The expression in parentheses is the Einstein tensor, so

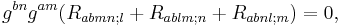
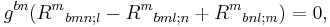
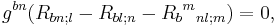
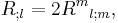
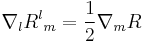$\nabla_l G^{lm} = 0,\,\!$ Q.E.D. (return to article)